1) Hertzscher Dipol
Bahnkurve der Ladung
| (1.1) |
Ladungsdichte
| (1.2) |
Strom
| (1.3) |
oder mit Bahnkurve
| (1.4) |
Vektorpotential
![Typesetting:-mprintslash([A_ = `+`(`/`(`*`(`/`(1, 4), `*`(mu[0], `*`(Int(Int(`/`(`*`(j_(rb_, tb), `*`(delta(`+`(t, `-`(`/`(`*`(r), `*`(c))), `-`(tb))))), `*`(Norm(`+`(rb_, `-`(r_))))), rb_ = `+`(`-`(i...](images_Hertz/Hertzscher_Dipol_5.gif) |
(1.5) |
Strahlungsfeld eines Hertzschen Dipols
(mit Maple)
Ein Hertzscher Dipol besteht aus einer negativen Punktladung am Koordinatenursprung und einer harmonisch bewegten positiven Punktladung auf a(t).
1) Hertzscher Dipol
Bahnkurve der Ladung
| (1.1) |
Ladungsdichte
| (1.2) |
Strom
| (1.3) |
oder mit Bahnkurve
| (1.4) |
Vektorpotential
![Typesetting:-mprintslash([A_ = `+`(`/`(`*`(`/`(1, 4), `*`(mu[0], `*`(Int(Int(`/`(`*`(j_(rb_, tb), `*`(delta(`+`(t, `-`(`/`(`*`(r), `*`(c))), `-`(tb))))), `*`(Norm(`+`(rb_, `-`(r_))))), rb_ = `+`(`-`(i...](images_Hertz/Hertzscher_Dipol_5.gif) |
(1.5) |
2) Vektorpotential in Nahfeldnäherung
Fernfeldnäherung
| (2.1) |
Einsetzen in Potential
![Typesetting:-mprintslash([A_ = `+`(`/`(`*`(`/`(1, 4), `*`(mu[0], `*`(Int(Int(`/`(`*`(j_(rb_, tb), `*`(delta(`+`(t, `-`(`/`(`*`(r), `*`(c))), `-`(tb))))), `*`(r)), rb_ = `+`(`-`(infinity)) .. infinity)...](images_Hertz/Hertzscher_Dipol_7.gif) |
(2.2) |
Einsetzen des Stromes
![Typesetting:-mprintslash([A_ = `+`(`/`(`*`(`/`(1, 4), `*`(mu[0], `*`(Int(Int(`+`(`-`(`/`(`*`(q, `*`(a[0], `*`(sin(`*`(omega, `*`(tb))), `*`(omega, `*`(_k, `*`(delta(`+`(rb_, `-`(`*`(a[0], `*`(cos(`*`(...](images_Hertz/Hertzscher_Dipol_8.gif) |
(2.3) |
Ausführen desIntegrals
| (2.4) |
In Basis der Kugelkoordinaten
| (2.5) |
3) B- und E-Feld:
Magnetisches Feld als Rotation des Vektorpotentials
| (3.1) |
also
![B_ = `+`(`-`(`/`(`*`(`/`(1, 4), `*`(mu[0], `*`(q, `*`(a[0], `*`(omega, `*`(sin(theta), `*`(`+`(`*`(omega, `*`(cos(`/`(`*`(omega, `*`(`+`(`-`(`*`(t, `*`(c))), r))), `*`(c))), `*`(r))), `-`(`*`(sin(`/`(...](images_Hertz/Hertzscher_Dipol_12.gif) |
(3.2) |
Rotation des B ist gleich der zeitlichen Änderung des E-Feldes, nach Zeitintagration also
| (3.3) |
Das heißt
![E_ = `+`(`-`(`/`(`*`(`/`(1, 2), `*`(mu[0], `*`(q, `*`(a[0], `*`(omega, `*`(cos(theta), `*`(_r, `*`(`+`(`-`(`*`(r, `*`(sin(`+`(`-`(`*`(omega, `*`(t))), `/`(`*`(omega, `*`(r)), `*`(c))))))), `-`(`/`(`*`...](images_Hertz/Hertzscher_Dipol_14.gif) ![E_ = `+`(`-`(`/`(`*`(`/`(1, 2), `*`(mu[0], `*`(q, `*`(a[0], `*`(omega, `*`(cos(theta), `*`(_r, `*`(`+`(`-`(`*`(r, `*`(sin(`+`(`-`(`*`(omega, `*`(t))), `/`(`*`(omega, `*`(r)), `*`(c))))))), `-`(`/`(`*`...](images_Hertz/Hertzscher_Dipol_15.gif) |
(3.4) |
4) Graphische Darstellung der Felder auf der x-Achse
Parameter:
| (4.1) |
x-z-Ebene in Kugelkoordinaten
| (4.2) |
y-Komponete des B-Feldes mit Parametern in XZ_Ebene
| (4.3) |
z-Komponente des E-Felder mit Parametern in XZ_Ebene
| (4.4) |
B_x und -E_z zum Vergleich von Nah- und Fernzone auf der x-Achse
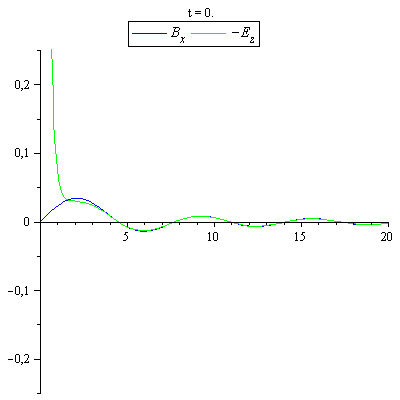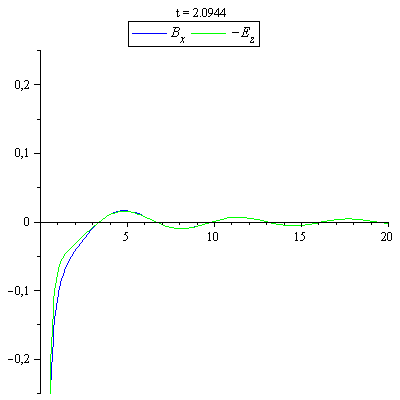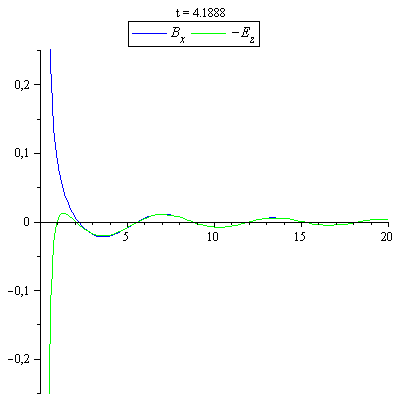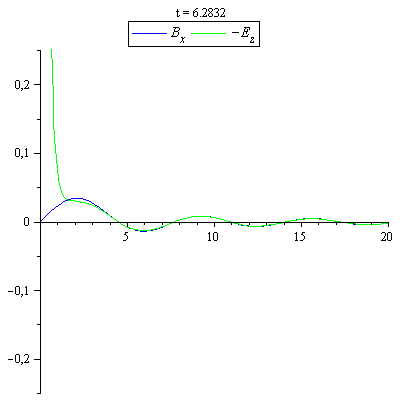 |
Bemerkung:
Die Felder wurden in der Fernfeldnäherung berechnet. Bei sehr kleinen Abständen sind die E- und B-Felder auch in dieser Näherung nicht in Phase.Man sieht in der Darstellung jedoch sehr schön, wie schnell sich die gemeinsame Phase in den Fernfeldern einstellt
3-D-Darstellung von By und Ez auf der x-Achse
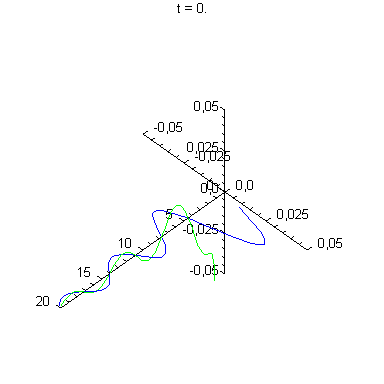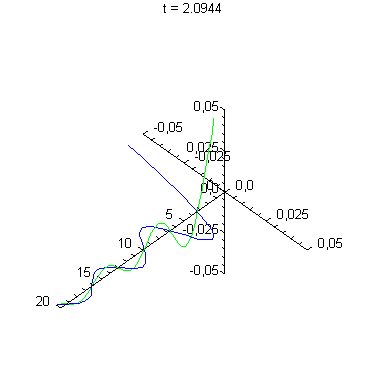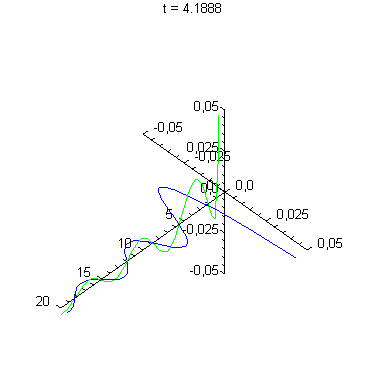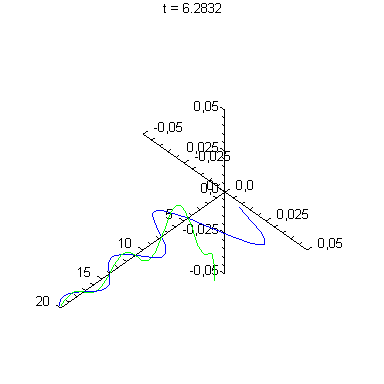 |
Das E-Feld schwingt in z-Richtung, das B-Feld in y-Richtung.
5) E-Feldlinien als Höhenlinien des B-Feldes in der x-z-Ebene
Definition der Feldlinien des E-Feldes:
| (5.1) |
Mit E-Feld
| (5.2) |
also
| (5.3) |
Beziehungsweise
| (5.4) |
In der x-z-Ebene ist
| (5.5) |
also
| (5.6) |
und
| (5.7) |
Die Feldlinien von E können in der x-z-Ebene also dargestellt werden als Höhenlininen von
| (5.8) |
6) Animation der Feldlinien des E-Feldes in der x-z-Ebene
B-Feld
![B_ = `+`(`-`(`/`(`*`(`/`(1, 4), `*`(mu[0], `*`(q, `*`(a[0], `*`(omega, `*`(sin(theta), `*`(`+`(`*`(omega, `*`(cos(`/`(`*`(omega, `*`(`+`(`-`(`*`(t, `*`(c))), r))), `*`(c))), `*`(r))), `-`(`*`(sin(`/`(...](images_Hertz/Hertzscher_Dipol_33.gif) |
(6.1) |
y-Komponente des B-Feldes
![B_y = `+`(`-`(`/`(`*`(`/`(1, 4), `*`(mu[0], `*`(q, `*`(a[0], `*`(`^`(omega, 2), `*`(sin(theta), `*`(cos(phi), `*`(cos(`/`(`*`(omega, `*`(`+`(`-`(`*`(t, `*`(c))), r))), `*`(c))))))))))), `*`(Pi, `*`(c,...](images_Hertz/Hertzscher_Dipol_34.gif) |
(6.2) |
Zeitintegral über B-Feld
| (6.3) |
also
![B[y, int] = `+`(`/`(`*`(`/`(1, 4), `*`(mu[0], `*`(q, `*`(a[0], `*`(omega, `*`(sin(theta), `*`(cos(phi), `*`(sin(`+`(`-`(`*`(omega, `*`(t))), `/`(`*`(omega, `*`(r)), `*`(c)))))))))))), `*`(Pi, `*`(c, `...](images_Hertz/Hertzscher_Dipol_36.gif) |
(6.4) |
x-z-Ebene:
![B[y, int] = `+`(`-`(`/`(`*`(`/`(1, 4), `*`(mu[0], `*`(q, `*`(a[0], `*`(omega, `*`(x, `*`(sin(`+`(`*`(omega, `*`(t)), `-`(`/`(`*`(omega, `*`(`^`(`+`(`*`(`^`(x, 2)), `*`(`^`(z, 2))), `/`(1, 2)))), `*`(c...](images_Hertz/Hertzscher_Dipol_37.gif) |
(6.5) |
Plot-Funktion
| (6.6) |
| (6.7) |
 |