![m = 1, hbar = 1, V[1] = 1, V[2] = -1, V[3] = -50](images_QM_Streu/04_QM_Streuproblem_1.gif){kind=small}
QM-Streuprobleme
1D am Kastenpotential
Parameter:
|
(1) |
1) Zeitunabhängige Schrödinger-Gleichung (ZSG)
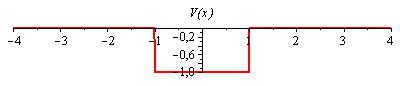
Kasten-Potential:
![V = piecewise(`<`(abs(x), 1), V[0], 0)](images_QM_Streu/04_QM_Streuproblem_2.gif){kind=small} |
(1.1) |
Graphische Darstellung des Potentials für V_0=1
 |
|
 |
Zeitunabhängige Schrödinger-Gleichung:
 |
(1.2) |
oder mit Potential
![`*`(E, `*`(u(x))) = `+`(`-`(`/`(`*`(`/`(1, 2), `*`(`^`(hbar, 2), `*`(diff(diff(u(x), x), x)))), `*`(m))), `*`(piecewise(`<`(abs(x), 1), V[0], 0), `*`(u(x))))](images_QM_Streu/04_QM_Streuproblem_6.gif) |
(1.3) |
2) Lösung der ZSG
2.1) Ansatz
x<-1: einlaufende und reflektierte Ebene Welle
|x|<1: Resonanzanteil der Welle
x>1: auslaufende (transmittierte) Welle
 |
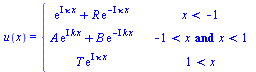(2.1.1) |
Einsetzen in die ZSG
  |
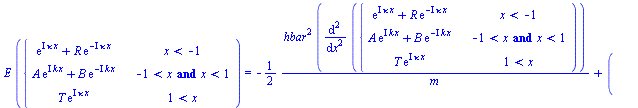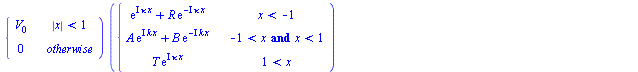(2.1.2) |
Wellenzahlen
für x>1
 |
(2.1.3) |
für |x|<1
 |
(2.1.4) |
Auflösen nach kappa und k
![kappa = `/`(`*`(`^`(2, `/`(1, 2)), `*`(`^`(`*`(E, `*`(m)), `/`(1, 2)))), `*`(hbar)), k = `/`(`*`(`^`(`+`(`*`(2, `*`(E, `*`(m))), `-`(`*`(2, `*`(V[0], `*`(m))))), `/`(1, 2))), `*`(hbar))](images_QM_Streu/04_QM_Streuproblem_12.gif){kind=small} |
(2.1.5) |
und einsetzen in das Quantenfeld
 |
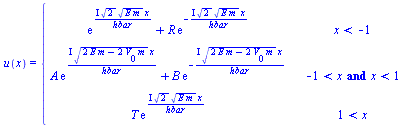(2.1.6) |
2.2) Bestimmung der Koeffizienten B, A, R, T
Stetigkeit links
 |
(2.2.1) |
also für obiges Quantenfeld
 |
(2.2.2) |
Stetigkeit rechts
 |
(2.2.3) |
also für obiges Quantenfeld
![`+`(`*`(A, `*`(exp(`/`(`*`(I, `*`(`^`(2, `/`(1, 2)), `*`(`^`(`+`(`-`(`*`(m, `*`(`+`(`-`(E), V[0]))))), `/`(1, 2))))), `*`(hbar))))), `*`(exp(`+`(`-`(`/`(`*`(`+`(I), `*`(`^`(2, `/`(1, 2)), `*`(`^`(`+`(...](images_QM_Streu/04_QM_Streuproblem_17.gif){kind=small} |
(2.2.4) |
Differenzierbarkeit links
 |
(2.2.5) |
also für obiges Quantenfeld
  |
(2.2.6) |
Differenzierbarkeit rechts
 |
(2.2.7) |
also für obiges Quantenfeld
![`/`(`*`(I, `*`(`^`(2, `/`(1, 2)), `*`(`+`(`*`(exp(`/`(`*`(I, `*`(`^`(2, `/`(1, 2)), `*`(`^`(`+`(`-`(`*`(m, `*`(`+`(`-`(E), V[0]))))), `/`(1, 2))))), `*`(hbar))), `*`(`^`(`+`(`-`(`*`(m, `*`(`+`(`-`(E),...](images_QM_Streu/04_QM_Streuproblem_22.gif) |
(2.2.8) |
2.3)Lösung des Gleichungssystems
Die analytische Formen Koeffezienten B.A.R.T sind sehr komplex. Es macht wenig Sinn, sie hier anzugeben. Sie werden aber vom Maple berechnet im Folgenden verwendet.
3) Streuphase Delta
Die Streuphase ist die Phase zwischen einlaufender und transmiitierten Welle. Sie enthält Informaiton über das Potential
 |
(3.1) |
Graphische Darstellung für verschiedene Potentialtiefen
 |
||||
|
Vor allem sieht man, ob das Potential repulsiv oder attraktiv ist und ob es Bindungszustände oder Resonanzen gibt.
4) Reflektions- und Transmissionskoeffizienten
Reflektions- und Transmissionskoeffizienten sind die Wahrscheinlichkeiten für Reflektion oder Transmission
 |
(4.1) |
Graphische Darstellung
|
Beim repulsiven Potential beginnt die Kurve mit Reflektion. Es gibt jedoch auch schon für Energien kleiner als V0 eine Tranmission, ein sogenanntes Tunneln.
Beim attraktiven Potential geht die Kurve sehr schnell in Transmission über.
Für große Energie wird das Potential in allen Fällen eher bedeutungslos.
5) Dichte
Dichte
 |
(5.1) |
|
Die Wahrscheinlichkeitsdichte zeigt in Abhängigkeit der Energie und Potentialtiefe ein sehr komplexes Verhalten
