Frequency Band of the f-mode Chandrasekhar-Friedman-Schutz Instability

Burkhard Zink, Oleg Korobkin, Erik Schnetter, Nikolaos Stergioulas

Movies demonstrating f-mode oscillations in a neutron star:
Ringing of a rapidly spinning neutron star
Ringing neutron star: cut through the equator

Gravitational wave detectors like LIGO, VIRGO, GEO-600 and TAMA-300 are expected to open a new window into the universe, one that is not based on electromagnetic radiation, but on radiation carried by the spacetime itself. However, even with the at present most advanced technology for laser interferometry, the tiny oscillations associated with gravitational waves are difficult to detect, and theoretical models of potential sources are of preeminent importance.

In the 1960s and 1970s, Chandrasekhar, Friedman and Schutz have found a new class of instability in stars, which is associated with the emission of gravitational radiation from oscillation modes. This effect, the CFS instability, is most effective in very compact configurations like neutron stars, and may be a substantial source of gravitational radiation detectable on Earth.

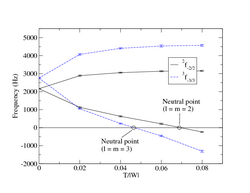
In this project, we have studied the oscillation spectrum of rapidly rotating neutron stars shortly after their birth with the help of large-scale numerical simulations. The instability is associated with a neutral point in the spectrum of nonaxisymmetric modes: on a sequence of models with increasing spin, the ultimately unstable mode is first traveling against the stellar rotation, but later "dragged" with the fluid to become co-rotating as seen from an inertial observer. It is this transition which makes the mode unstable to the CFS mechanism.

All simulations have been performed in full general relativity, that is, with full consideration for solving Einstein's field equations. We have employed the nonlinear GRMHD code THOR for this purpose, with neutron star models constructed using the publicly available RNS code. Each model was perturbed with a small density adjustment to excite the oscillation modes, and the spectrum is subsequently obtained from time evolution and data analysis. A result for a particular sequence of models for both the l = m = 2 and l = m = 3 mode order is shown in the figure above.

Earlier studies of this type have already been performed with an accurate linear evolution code in the Cowling approximation, i.e. in a case where the spacetime is not allowed to dynamically adjust to the stellar motions. Direct comparisons show that the differences between a fully relativistic simulation and the Cowling approximation are most significant for the lowest order l = m = 2 mode, in the sense that a dynamical spacetime enhances the instability. These differences will then be smaller for unstable modes of higher order.

References
Gaertig, E., Kokkotas, K.D. (2008). Oscillations of rapidly rotating relativistic stars. Phys. Rev. D, 78, 064063.
Zink, B., Korobkin, O., Schnetter, E., Stergioulas, N. (2010). Frequency band of the f-mode Chandrasekhar-Friedman-Schutz instability. Phys. Rev. D, 81, 084055.